Function Reconstruction

Figure 3.3: Two dimensional sampling in the space and frequency domain [29]. In the space domain (top), sampling corresponds to the multiplication of the original function with an impulse grid. In the frequency domain (bottom), sampling corresponds to the convolution with an impulse grid.

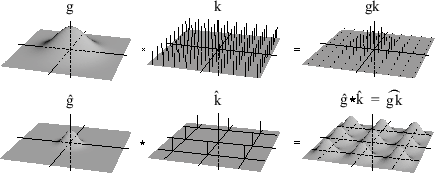
A point sample can be represented as a scaled Dirac impulse function. Sampling a signal is equivalent to multiplying it by a grid of impulses, one at each sample point, as shown in Figure 3.3 [29]. The Fourier transform of a two-dimensional impulse grid with frequency $f_x$ in $x$ and $f_y$ in $y$ is itself a grid of impulses with period $f_x$ in $x$ and $f_y$ in $y$. If we call the impulse grid $k(x,y)$ and the signal $g(x,y)$, then the Fourier transform of the sampled signal, $\hat{gk}$, is $\hat{g} * \hat{k}$. Since $k$ is an impulse grid, convolving $\hat{g}$ with $\hat{k}$ amounts to duplicating $\hat{g}$ at every point of $\hat{k}$, producing the spectrum shown at bottom right in Figure 3.3. The copy of $\hat{g}$ centered at zero is the primary spectrum, and the other copies are called alias spectra. If $\hat{g}$ is zero outside a small enough region that the alias spectra do not overlap the primary spectrum, then $\hat{g}$ can be recovered by multiplying $\hat{gk}$ by a function $\hat{h}$ which is one inside that region and zero elsewhere. Such a multiplication is equivalent to convolving the sampled data $gk$ with $h$, the inverse transform of $\hat{h}$. This convolution with $h$ allows us to reconstruct the original signal $g$ by removing, or filtering out, the alias spectra, so we call $h$ a reconstruction filter.

Thus, the goal of reconstruction is to extract the primary spectrum and to suppress the alias spectra. Since the primary spectrum comprises the low frequencies, the reconstruction filter is a low-pass filter. It is clear from Figure 3.3 that the simplest region to which we could limit $\hat{g}$ is the region of frequencies that are less than half the sampling frequency along each axis. We call this limiting frequency the Nyquist frequency and the region the Nyquist region. An ideal reconstruction filter can then be defined to have a Fourier transform that has the value one in the Nyquist region and zero outside it.

Extending the above to three-dimensional signals as used in volume rendering, the sampling grid becomes a three-dimensional lattice and the Nyquist region a cube. Given this Nyquist region, the ideal convolution filter is the inverse transform of a cube, which is the product of three sinc functions.

$$h_I (x,y,z) = (2f_N )^3 {\mathop{\rm sinc}\nolimits}(2f_N x... ...m sinc}\nolimits}(2f_N y) {\mathop{\rm sinc}\nolimits}(2f_N z)$$ (3.1)

Thus, in principle, a volume signal can be exactly reconstructed from its samples by convolving with $h_I$. In practice, however, $h_I$ cannot be implemented, because it has infinite extent in the spacial domain. Practical filters will therefore introduce some artifacts into the reconstructed function. A practical filter takes a weighted sum of a limited number of samples to compute the reconstruction of a point. That is, it is zero outside some finite region. This region is called the region of support. Filters with a larger region of support are generally more expensive since more samples have to be weighted.

The simplest interpolation function is known as zero-order interpolation, which is actually just a nearest neighbor function. The value at any location is simply the value of the closest sample to that location. One common interpolation function is a piecewise function known as first-order interpolation, or trilinear interpolation. With this function, the value is assumed to vary linearly along directions parallel to one of the major axes. Let the point $p$ lie at location $(x_p,y_p,z_p)^T$ within a cubic cell and let $v_{000},...,v_{111}$ be the sample values at the eight corners of the cell. The value $v_p$ at location $p$, according to trilinear interpolation, is then:

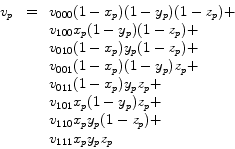$$\begin{array}{rcl} v_p &=& v_{000} (1 - x_p )(1 - y_p )(1 - ... ...p y_p (1 - z_p ) + \\ & & v_{111} x_p y_p z_p \\ \end{array}$$ (3.2)

Marschner and Lobb [29] have examined various reconstruction filters. The best results were achieved with windowed sinc filters. While they provide superior reconstruction quality, they are also about two orders of magnitude more expensive than trilinear interpolation. Therefore, when interactive performance is desired, trilinear reconstruction is often the method of choice.