


Next: System analysis near trajectories
Up: Notes on the local
Previous: Interpreting linear dynamical systems
Subsections
Linear systems by themselves have a rather simple dynamical
behavior. The reason, why linear system analysis is so important,
is that non-linear systems are often analyzed by local
linearization [83], i.e., a non-linear function
is approximated (locally) by a linear function. Linearization is
typically done by using a Taylor expansion of a function and
neglecting the higher-order terms. See Eq. 3.14 for Taylor
expansion of a scalar function
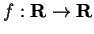 ,
Eq. 3.15 shows the Taylor expansion for a vector function
,
Eq. 3.15 shows the Taylor expansion for a vector function
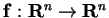 .
This kind of analysis is
especially easy near critical points, since the long-term behavior
trivially coincides with the local behavior at these points.
.
This kind of analysis is
especially easy near critical points, since the long-term behavior
trivially coincides with the local behavior at these points.
| f(c+d) |
= |
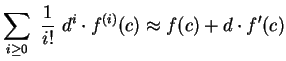 |
(3.13) |
| f(c+d) |
= |
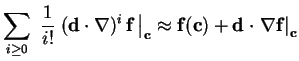 |
(3.14) |
Analyzing the system's behavior near its critical points can help
to understand the evolution of any state of the system. Assuming
the system is non-linear and hyperbolic, linearization can be used
to determine the behavior near critical points completely.
Continuous and discrete systems can be treated rather
similar [72] (See Tab. 3.2).
Table 3.2:
Local linearization near critical points
| |
continuous case |
discrete case |
|
| vector field def. |
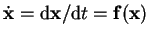 |
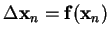 |
(a) |
| critical point def. |
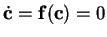 |
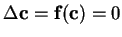 |
(b) |
| re-writing
x,
xn |
x = c+d |
xn = c+dn |
(c) |
| using Taylor exp. |
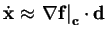 |
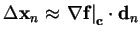 |
(d) |
| linearized system |
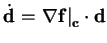 |
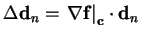 |
(e) |
|
To keep the analysis simple, we assume the system to be autonomous
and time-independent (see Tab. 3.2(a) for the
definitions). Assuming the existence of at least one critical
point (see Tab. 3.2(b) for the definitions) any
state of the dynamical system near critical point
c can
be rewritten with respect to
c (see
Tab. 3.2(c)).
With this reformulation the dynamical system can be approximated
by a Taylor expansion as shown in Tab. 3.2(d).
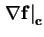 denotes the Jacobian matrix of
f(x) evaluated at
c. Using
Tab. 3.2(c) again, the left side of the Taylor
expansion in Tab. 3.2(d) can be rewritten.
This operation yields the
linearized systems for small perturbations around critical point
c (see Tab. 3.2(e)). These linear
systems can now be analyzed as discussed in the last section.
denotes the Jacobian matrix of
f(x) evaluated at
c. Using
Tab. 3.2(c) again, the left side of the Taylor
expansion in Tab. 3.2(d) can be rewritten.
This operation yields the
linearized systems for small perturbations around critical point
c (see Tab. 3.2(e)). These linear
systems can now be analyzed as discussed in the last section.
Cycles are another important class of characteristic subsets
within continuous dynamical systems. A cycle is given, when the
system returns to a previous state. The system behavior near such
a cycle can be analyzed by using a Poincaré map. Such a map is
a discrete dynamical system, that is produced from a continuous
dynamical system and that is of a lower dimension than the
original system. A Poincaré map is specified by the
cross-section of a surface perpendicular to the cycle (usually a
plane) and a trajectory near the cycle. The Poincaré map is a
discrete dynamical system with at least one critical point
c, i.e.,
c is the intersection of the cycle
and the surface. Thus the
Poincaré map can be analyzed as shown in the section before and
the results are then used for interpreting the system's behavior
nearby the cycle [72].



Next: System analysis near trajectories
Up: Notes on the local
Previous: Interpreting linear dynamical systems
Helwig Löffelmann, November 1998, mailto:helwig@cg.tuwien.ac.at.
![]() ,
Eq. 3.15 shows the Taylor expansion for a vector function
,
Eq. 3.15 shows the Taylor expansion for a vector function
![]() .
This kind of analysis is
especially easy near critical points, since the long-term behavior
trivially coincides with the local behavior at these points.
.
This kind of analysis is
especially easy near critical points, since the long-term behavior
trivially coincides with the local behavior at these points.
![]() denotes the Jacobian matrix of
f(x) evaluated at
c. Using
Tab. 3.2(c) again, the left side of the Taylor
expansion in Tab. 3.2(d) can be rewritten.
This operation yields the
linearized systems for small perturbations around critical point
c (see Tab. 3.2(e)). These linear
systems can now be analyzed as discussed in the last section.
denotes the Jacobian matrix of
f(x) evaluated at
c. Using
Tab. 3.2(c) again, the left side of the Taylor
expansion in Tab. 3.2(d) can be rewritten.
This operation yields the
linearized systems for small perturbations around critical point
c (see Tab. 3.2(e)). These linear
systems can now be analyzed as discussed in the last section.