


Next: Discussion
Up: Notes on the local
Previous: Analysis near critical points
In the following we propose another approach to analyze a
dynamical system's behavior. It is somewhat similar to the method
by de Leeuw and van Wijk [19], as the dynamical system
is also transformed into the Frenét-Frame 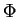 of a point on
the trajectory. Contrary to their approach we use the analysis by
eigenvalues and eigenvectors to interpret this transformed
Jacobian matrix. Expressing a dynamical system
of a point on
the trajectory. Contrary to their approach we use the analysis by
eigenvalues and eigenvectors to interpret this transformed
Jacobian matrix. Expressing a dynamical system
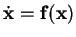 in terms of
in terms of 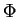 one
gets
one
gets
Near the point of interest
p (represented in the global
coordinate system) a state of the system can be written as
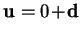 in terms of the local coordinate system.
Note, that
p represented in terms of
in terms of the local coordinate system.
Note, that
p represented in terms of 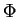 is 0.
Using a Taylor expansion of
is 0.
Using a Taylor expansion of
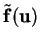 up to
first-order terms, we get
up to
first-order terms, we get
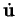 |
= |
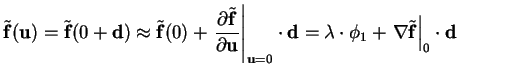 |
(3.16) |
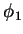 |
 |
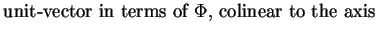 |
|
| |
|
corresponding to the
trajectory's tangent |
|
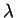 |
 |
length of f(p) |
|
Note, that
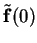 can be written as
can be written as
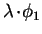 ,
since the first axis of the local
coordinate system (Frenét-Frame) is specified to be colinear to
the flow. Transforming the left-most side of Eq. 3.17 by
using
,
since the first axis of the local
coordinate system (Frenét-Frame) is specified to be colinear to
the flow. Transforming the left-most side of Eq. 3.17 by
using
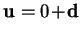 we get a linearized system for small
perturbations of
p (in terms of
we get a linearized system for small
perturbations of
p (in terms of 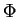 ), because
), because
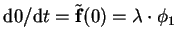 .
.
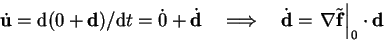 |
(3.17) |
Now perturbations that are especially useful to
analyze are investigated. The elements of
d can be
separated into a scalar
d[1] and a vector
![$\mathbf{d}[2\ldots]$](img147.gif) that is of one dimension less than
d.
d[1] is assumed to be 0, since perturbations of
p that are not perpendicular to the trajectory's
tangent make no sense at all - a state of the
system that is represented as a perturbation of
p with
a component
that is of one dimension less than
d.
d[1] is assumed to be 0, since perturbations of
p that are not perpendicular to the trajectory's
tangent make no sense at all - a state of the
system that is represented as a perturbation of
p with
a component
![$\mathbf{d}[1]\!\ne\!0$](img148.gif) usually can be more accurately
expressed as
a (perpendicular) perturbation of another point on exactly the
same trajectory.
Thus
usually can be more accurately
expressed as
a (perpendicular) perturbation of another point on exactly the
same trajectory.
Thus
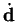 does not depend on the first row of matrix
does not depend on the first row of matrix
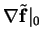 .
The remaining elements of
.
The remaining elements of
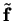 's Jacobian
's Jacobian
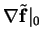 can be
decomposed into the first line
can be
decomposed into the first line
![$\nabla\tilde{\mathbf{f}}\vert _0[1,2\ldots]$](img152.gif) and the lower-right
sub-matrix
and the lower-right
sub-matrix
![$\nabla\tilde{\mathbf{f}}\vert _0[2\ldots,2\ldots]$](img153.gif) .
.
Decomposing
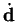 similar to
d yields a part
parallel to the trajectory's tangent (scalar
similar to
d yields a part
parallel to the trajectory's tangent (scalar
![$\dot{\mathbf{d}}[1]$](img154.gif) )
and a part perpendicular to a (sub-vector
)
and a part perpendicular to a (sub-vector
![$\dot{\mathbf{d}}[2\ldots]$](img155.gif) ):
):
![\begin{displaymath}\begin{array}{rcrcl}
\dot{\mathbf{d}}[1]
&=& \left.\nabla\t...
...2\ldots]
&=& \mathbf{A}\cdot{\mathbf{d}}[2\ldots]
\end{array}\end{displaymath}](img156.gif) |
(3.18) |
We now have a locally linearized system
(
![$\dot{\mathbf{d}}[2\ldots]=\mathbf{A}\cdot{\mathbf{d}[2\ldots]}$](img157.gif) )
that describes the
evolution of variations orthogonal to the flow. The system has
one dimension less than the original system. Matrix
A can be
analyzed as already shown for continuous systems at the
neighborhood of critical points. But we must be careful with the
interpretation of this analysis, because all the results hold for
the investigated point
p only.
For example, if the analysis of
matrix
A reveals that the system's evolution is
convergent (critical point is an attractor) the only thing that
can be said is that
nearby trajectories are locally attracted by the trajectory at the
specific location chosen. To detect convergent, divergent, or
saddle regions of a trajectory it must be shown that the
structural characteristics of matrix
A are persistent
for a certain region of the trajectory. This might be not simple
analytically, but can be done approximately by numerical simulation.
)
that describes the
evolution of variations orthogonal to the flow. The system has
one dimension less than the original system. Matrix
A can be
analyzed as already shown for continuous systems at the
neighborhood of critical points. But we must be careful with the
interpretation of this analysis, because all the results hold for
the investigated point
p only.
For example, if the analysis of
matrix
A reveals that the system's evolution is
convergent (critical point is an attractor) the only thing that
can be said is that
nearby trajectories are locally attracted by the trajectory at the
specific location chosen. To detect convergent, divergent, or
saddle regions of a trajectory it must be shown that the
structural characteristics of matrix
A are persistent
for a certain region of the trajectory. This might be not simple
analytically, but can be done approximately by numerical simulation.



Next: Discussion
Up: Notes on the local
Previous: Analysis near critical points
Helwig Löffelmann, November 1998, mailto:helwig@cg.tuwien.ac.at.
![]() similar to
d yields a part
parallel to the trajectory's tangent (scalar
similar to
d yields a part
parallel to the trajectory's tangent (scalar
![]() )
and a part perpendicular to a (sub-vector
)
and a part perpendicular to a (sub-vector
![]() ):
):