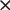In the previous section various fields of applications of visualization briefly have been presented. The work presented here closely fits into the flow visualization area, since flow data and dynamical systems match up quite good with respect to visualization - many techniques developed for flow visualization are useful for dynamical system visualization and vica versa.
Dynamical systems are a
description of the evolution of some (usually inter-dependent)
entities within a common system. A food chain, for
instance, describing the who-eats-whom relation between several
species, sharing some common place of living, is modeled as
a dynamical system.
The
predator-prey model by Lotka and Volterra [72]
is an example of such a food chain.
It describes the evolution of a system consisting of one species
of consumers (predators) and another one of resource (prey).
Basically, it consists of two numbers representing the amount
of both species present in the system at a certain time, and
a description of the temporal change of these numbers due to
the given setting of the system.
More general, a dynamical system is a set of
n numbers
x[i] - usually n is called the
dimensionality of the system - that vary according to specific
set of rules. These system variables
x[i] build
up the state
![]() of the
system, where
of the
system, where ![]() usually is called the phase space of
the dynamical system. Some specific value
x(t) represents the actual configuration of the system at a specific
point in time t.
In addition to system variables and time, usually
parameters
p[j] are part of the rules of
evolution. Their different values span a class of
dynamical systems over
usually is called the phase space of
the dynamical system. Some specific value
x(t) represents the actual configuration of the system at a specific
point in time t.
In addition to system variables and time, usually
parameters
p[j] are part of the rules of
evolution. Their different values span a class of
dynamical systems over ![]()
![]() Rm, called
parameter space.
Rm, called
parameter space.
A continuous dynamical system usually is
given by a set of ordinary differential
equations (ODEs) [4], whereas a discrete
dynamical system is specified by difference equations:
A dynamical system is called time-dependent, if the rules determining the dynamics depend on time, i.e., fp itself depends on time t (see Eqs. 1.1). If, on the other hand, these rules are static over time, a steady, i.e., a time-independent system is given. In this case fp only depends on the present state of the system x(t) and parameters p.
In the case of the Lotka and Volterra model, a two-dimensional,
continuous, and steady dynamical system is given: the
state
![]() of the system is
composed of x (amount of prey) and y (predators), and two ODEs including four parameters that represent
the rules of evolution:
of the system is
composed of x (amount of prey) and y (predators), and two ODEs including four parameters that represent
the rules of evolution:
Solutions of a dynamical system, i.e., solutions to the
differential or difference equations, are called
trajectories or orbits. For continuous and steady
dynamical systems a trajectory
![]() starts at a
specific seed value
s and evolves over time according
to the following equation:
starts at a
specific seed value
s and evolves over time according
to the following equation:
![\framebox[\textwidth]{
\begin{tabular*}{.93\linewidth}{@{}@{\extracolsep{\fill}...
...e=0.61]{figs/lvm-tailor.eps}
\\ {\small{}(a)}
& {\small{}(b)}
\end{tabular*}}](img36.gif) |
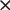 R - time is added as an additional dimension - or
R - time is added as an additional dimension - or