


Next: NLCYC1
Up: Sample dynamical systems
Previous: COMPLFP
For testing Poincaré maps we define a simple cycle in 3D. The
critical point of the
Poincaré map of this dynamical system should be either an
attracting node, a saddle, or a repelling node. For this purpose
we think about points in phase space as specified by coordinates
r, 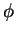 ,
and z: r and
,
and z: r and 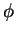 denote polar coordinates in
the x-y plane. REALCYC can now be specified as follows:
denote polar coordinates in
the x-y plane. REALCYC can now be specified as follows:
This dynamical system
contains a cycle. This is easy to show:
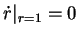 and
and
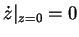 induce that the unit cycle
induce that the unit cycle
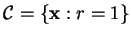 is a cycle of this dynamical system.
Furthermore it can be stated that there are no other cycles than
is a cycle of this dynamical system.
Furthermore it can be stated that there are no other cycles than
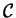 in this specific dynamical system:
since
in this specific dynamical system:
since
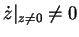 no cycle can exist outside the
x-y plane;
no cycle can exist outside the
x-y plane;
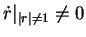 assures that no other
cycle than the unit cycle resides within the x-y plane.
assures that no other
cycle than the unit cycle resides within the x-y plane.
Using this definition, we can directly influence the Poincaré
map of cycle
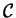 by adjusting parameters A and B:
by adjusting parameters A and B:
To embed this system in the scope of DynSys3D, it has to be
defined on the basis of Cartesian coordinates:
| x |
= |
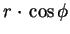 |
|
| y |
= |
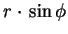 |
|
The dynamical system in terms of Cartesian coordinates is then
given as:



Next: NLCYC1
Up: Sample dynamical systems
Previous: COMPLFP
Helwig Löffelmann, November 1998, mailto:helwig@cg.tuwien.ac.at.
![]() by adjusting parameters A and B:
by adjusting parameters A and B: