


Next: REALTORUS
Up: Sample dynamical systems
Previous: REALCYC
Another test case for the Poincaré section techniques is
NLCYC1, which is a dynamical system that exhibits one cycle
with a non-linear Poincaré map.
First we specify a linear 2D system with a critical point in the
origin and characteristic directions coinciding with the axes of
the system:
Next we apply a non-linear transformation to
variable 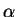 :
:
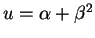 ,
and
,
and 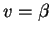 .
This
transformation yields
another 2D dynamical
system as follows:
.
This
transformation yields
another 2D dynamical
system as follows:
We now place the entire system into the half-plane
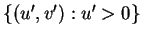 by
transformation
by
transformation
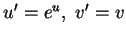 (
(
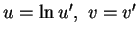 )
and end up with
the following system:
)
and end up with
the following system:
Finally we transform the system into 3D by rotating it around the
z-axis (r=u',
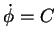 ,
and z=v'). This yields the
final system as follows:
,
and z=v'). This yields the
final system as follows:



Next: REALTORUS
Up: Sample dynamical systems
Previous: REALCYC
Helwig Löffelmann, November 1998, mailto:helwig@cg.tuwien.ac.at.