


Next: Notes on the notation
Up: Sample dynamical systems
Previous: NLCYC1
REALTORUS should be a dynamical system, which exhibits an invariant
torus, either attracting or repelling. To design this system, we
start in 2D:
Depending on the value of A this system has either an attracting
or repelling cycle of radius R. In Cartesian coordinates
(
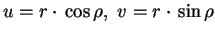 )
this
system is given as follows:
)
this
system is given as follows:
We now squeeze this system into half-plane
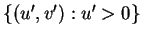 by
transformation
by
transformation
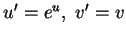 (
(
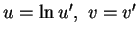 )
and end up with
the following system:
)
and end up with
the following system:
Using this dynamical system in 2D, we can construct a
three-dimensional system, which actually contains an invariant
torus by the following definition:
| x |
= |
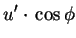 |
|
| y |
= |
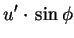 |
|
| z |
= |
v' |
|
Assuming
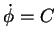 (
(
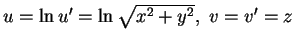 )
this dynamical system can be expressed as follows:
)
this dynamical system can be expressed as follows:



Next: Notes on the notation
Up: Sample dynamical systems
Previous: NLCYC1
Helwig Löffelmann, November 1998, mailto:helwig@cg.tuwien.ac.at.