


Next: Interpreting linear dynamical systems
Up: Notes on the local
Previous: Differential geometry and terms
This section discusses some of the often used terms in combination
with dynamical system analysis. Most of the terms might be
well-known to the reader, but often several differing terms are
used in literature to denote the same concept or object. To avoid
possible confusion about these sometimes interchangeably used
terms a clarifying survey is appropriate.
We start with operator  ,
which is often used to define other
important terms for the analysis of dynamical systems. It builds
up a vector of the partial derivatives of its operand and is
defined as shown in Eq. 3.3 [13].
If
,
which is often used to define other
important terms for the analysis of dynamical systems. It builds
up a vector of the partial derivatives of its operand and is
defined as shown in Eq. 3.3 [13].
If  's operand
f(x) is a scalar function, then
's operand
f(x) is a scalar function, then
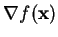 is called the gradient of f [13].
If
is called the gradient of f [13].
If  's operand
f(x) is a vector
function, then
's operand
f(x) is a vector
function, then
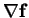 is the Jacobian matrix
is the Jacobian matrix
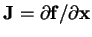 of
f(x) [19].
of
f(x) [19].
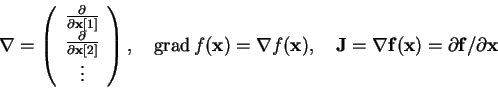 |
(3.2) |
An often used (scalar) term is the divergence of a flow
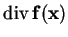 .
It can
be written as
.
It can
be written as
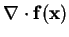 or as the trace
or as the trace
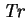 of
f's Jacobian
of
f's Jacobian
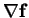 [13]:
[13]:
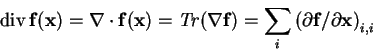 |
(3.3) |
The divergence basically describes the local amount of outgoing or
incoming flow at a specific location of the dynamical system. It
is 0, if the amount of incoming flow is equal to the amount of
outgoing flow.
Another important term for the local analysis of dynamical systems
is the rotation vector of a flow:
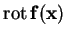 [61,75].
This attribute of a flow is often named vorticity instead of
rotation and abbreviated by
[61,75].
This attribute of a flow is often named vorticity instead of
rotation and abbreviated by 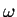 [29].
As a third term sometimes curl is used instead of
rotation [29].
The vorticity/rotation/curl of a flow is defined as follows:
[29].
As a third term sometimes curl is used instead of
rotation [29].
The vorticity/rotation/curl of a flow is defined as follows:
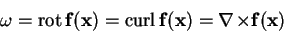 |
(3.4) |
Vector
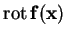 describes the
rotation axis and its length the rotation
velocity, which is given at state
x. Note, that some
references define the vorticity slightly different as
describes the
rotation axis and its length the rotation
velocity, which is given at state
x. Note, that some
references define the vorticity slightly different as
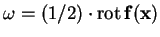 .
.
A scalar term related to the vorticity as defined above is the
stream vorticity 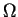 [29,75].
It is the cosine of the angle enclosed by the vorticity vector
and the flow vector
f(x).
This term characterizes the type of rotation in the system. If
[29,75].
It is the cosine of the angle enclosed by the vorticity vector
and the flow vector
f(x).
This term characterizes the type of rotation in the system. If
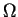 is 1, the flow rotates around the flow vector
f(x), whereas
a value of 0 implies, that either there is no vorticity or the
flow rotates in a plane which also contains the direction of the flow.
is 1, the flow rotates around the flow vector
f(x), whereas
a value of 0 implies, that either there is no vorticity or the
flow rotates in a plane which also contains the direction of the flow.
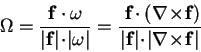 |
(3.5) |
Just slightly different from the above definition is the
specification of helicity [19]. Furthermore the
helicity density Hd as given in the literature is just the same
as helicity [67]. A value of 0 means exactly the
same as no stream vorticity, but helicity increases proportional
to the length of 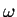 and
f. It is defined by:
and
f. It is defined by:
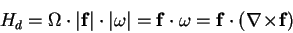 |
(3.6) |



Next: Interpreting linear dynamical systems
Up: Notes on the local
Previous: Differential geometry and terms
Helwig Löffelmann, November 1998, mailto:helwig@cg.tuwien.ac.at.
![]() ,
which is often used to define other
important terms for the analysis of dynamical systems. It builds
up a vector of the partial derivatives of its operand and is
defined as shown in Eq. 3.3 [13].
If
,
which is often used to define other
important terms for the analysis of dynamical systems. It builds
up a vector of the partial derivatives of its operand and is
defined as shown in Eq. 3.3 [13].
If ![]() 's operand
f(x) is a scalar function, then
's operand
f(x) is a scalar function, then
![]() is called the gradient of f [13].
If
is called the gradient of f [13].
If ![]() 's operand
f(x) is a vector
function, then
's operand
f(x) is a vector
function, then
![]() is the Jacobian matrix
is the Jacobian matrix
![]() of
f(x) [19].
of
f(x) [19].
![]() [61,75].
This attribute of a flow is often named vorticity instead of
rotation and abbreviated by
[61,75].
This attribute of a flow is often named vorticity instead of
rotation and abbreviated by ![]() [29].
As a third term sometimes curl is used instead of
rotation [29].
The vorticity/rotation/curl of a flow is defined as follows:
[29].
As a third term sometimes curl is used instead of
rotation [29].
The vorticity/rotation/curl of a flow is defined as follows:
![]() [29,75].
It is the cosine of the angle enclosed by the vorticity vector
and the flow vector
f(x).
This term characterizes the type of rotation in the system. If
[29,75].
It is the cosine of the angle enclosed by the vorticity vector
and the flow vector
f(x).
This term characterizes the type of rotation in the system. If
![]() is 1, the flow rotates around the flow vector
f(x), whereas
a value of 0 implies, that either there is no vorticity or the
flow rotates in a plane which also contains the direction of the flow.
is 1, the flow rotates around the flow vector
f(x), whereas
a value of 0 implies, that either there is no vorticity or the
flow rotates in a plane which also contains the direction of the flow.