| = | 0 | (3.7) | |
| = | (3.8) |
As already stated previously, linear dynamical systems are especially simple to analyze. Since we need this procedure for the rest of this chapter, we briefly discuss some different approaches of analyzing the matrix of a linear and autonomous dynamical system's matrix A [83].
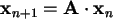 )
that are
autonomous and linear can be entirely analyzed by
investigating the matrix
A and its characteristics.
One possibility
is to compute
A's eigenvalues and its eigenvectors from
Eqs. 3.8 and 3.9,
respectively [72,83]. The
knowledge of
A's eigenvalues and eigenvectors is always
sufficient to describe the qualitative behavior of a linear system.
)
that are
autonomous and linear can be entirely analyzed by
investigating the matrix
A and its characteristics.
One possibility
is to compute
A's eigenvalues and its eigenvectors from
Eqs. 3.8 and 3.9,
respectively [72,83]. The
knowledge of
A's eigenvalues and eigenvectors is always
sufficient to describe the qualitative behavior of a linear system.
The interpretation of the eigenvalues ![]() - they can be
either real or complex - is different for continuous and discrete
dynamical systems, because a continuous system is specified by the
change of the current state, whereas a discrete dynamical system
is specified by giving the next state of the system (see
Tab. 3.1).
- they can be
either real or complex - is different for continuous and discrete
dynamical systems, because a continuous system is specified by the
change of the current state, whereas a discrete dynamical system
is specified by giving the next state of the system (see
Tab. 3.1).
|
Convergence, divergence, and rotation are to be interpreted
relatively to the origin of the coordinate system. Note, that a
critical point of a continuous dynamical system is called hyperbolic,
if its eigenvalues do not lie on the imaginary axis
(
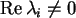 ).
Critical points of discrete dynamical systems are hyperbolic, if
).
Critical points of discrete dynamical systems are hyperbolic, if
![]() for all eigenvalues.
for all eigenvalues.
Remaining elements of matrix
Jlocal, that are
marked with either `![]() ' alone or `
' alone or `![]() ' and
`
' and
`![]() ', specify the changes of the flow that are
perpendicular to
f(x). Splitting the
bottom-right 2
', specify the changes of the flow that are
perpendicular to
f(x). Splitting the
bottom-right 2 2-matrix into a
symmetric and an asymmetric one gives the divergence (by the
elements marked with `
2-matrix into a
symmetric and an asymmetric one gives the divergence (by the
elements marked with `![]() ') and the torsion (by the elements
marked with `
') and the torsion (by the elements
marked with `![]() ') of the flow.
') of the flow.